FEMAXX (Finite Element Maxwell Eigensolver): src/h5

Go to the source code of this file.


Functions
Epetra_Map *	h5_write_eigenfield_retrieve_DoF_robust (const Epetra_MultiVector &Q, const Epetra_Comm &comm)
	Implementation file for HDF5 tools functionality.
Epetra_Map *	h5_write_eigenfeield_retrieve_DoF_efficient (const std::string &file_name, const Epetra_Comm &comm, mesh::TetMesh tetmesh, NedelecMesh &nedelecmesh, const Epetra_MultiVector &Q, double lambda)
void	h5_write_eigenfield_write_hdf5e (const std::string &file_name, const Epetra_Comm &comm, int lntet, int gntet, int mthmode, double *ev)
void	h5_write_eigenfield_write_hdf5h (const std::string &file_name, const Epetra_Comm &comm, int lntet, int gntet, int mthmode, double *hv)
void	h5_write_eigenfield_writehdf5sloc (const std::string &file_name, const Epetra_Comm &comm, int ntet, int gntet, double *sloc)
void	h5_compute_eigenquality (const std::string &file_name, const Epetra_Comm &comm, mesh::TetMesh tetmesh, NedelecMesh &nedelecmesh, const Epetra_MultiVector &Q, double lambda, double *&quality)
	Compute the quality factor associated with an eigenmode and store it into the HDF5 file.
void	h5_cartesian_sampling (const std::string &file_name, const Epetra_Comm &comm, mesh::TetMesh tetmesh, NedelecMesh &nedelecmesh, const Epetra_MultiVector &Q, double lambda, double xmin, double xmax, int nx, double ymin, double ymax, int ny, double zmin, double zmax, int nz)
	evaluate the eigenmodal solution on a cartesian grid
void	h5_cartesian_sampling_write_hdf5 (const Epetra_Comm &comm, const std::string &file_name, unsigned int nmode, std::vector< std::vector< std::vector< unsigned int > > > &exists, std::vector< std::vector< std::vector< std::vector< mesh::Vector3 > > > > &efield, std::vector< std::vector< std::vector< std::vector< mesh::Vector3 > > > > &hfield, double xmin, double xmax, const int nx, double ymin, double ymax, const int ny, double zmin, double zmax, const int nz)
	processorwise store the eigenmodal solution, sampled on a cartesian grid, into the hdf5 file; nota bene: because the sequence of access to the hdf5 file is in no way ordered, we must make sure that spatial positions marked as existent by one processor are not overwritten as non-existent by another processor. This is ensured as follows: (1) the root process only initializes the complete 3-dimensional boolean array as false (2) all processors only write into the file if the respective boolean flag signals that the position exists on the local processor; otherwise they do nothing to the hdf5 file.
void	h5_create_empty_file (const std::string &file_name)
void	h5_write_param_list (const std::string &file_name, const Teuchos::ParameterList &params)
void	h5_read_param_list (const std::string &file_name, Teuchos::ParameterList &params)
void	h5_write_eigenmodes (const std::string &file_name, const Epetra_MultiVector &Q, const Epetra_SerialDenseVector &lambda)
void	h5_read_eigenmodes (const std::string &file_name, Epetra_MultiVector Q, Epetra_SerialDenseVector lambda)
void	h5_read_eigenmodes (const std::string &file_name, colarray::Matrix< double > &Q, colarray::ColumnVector< double > &lambda)
void	h5_read_eigenmesh (const std::string &file_name)
void	h5_write_eigenmesh (const std::string &file_name, const Epetra_Comm &comm, mesh::TetMesh *tetmesh)
void	h5_write_eigenpoint (const std::string &file_name, const Epetra_Comm &comm, mesh::TetMesh *tetmesh)
	Write the tetrahedral point coordinates in parallel mode, ensuring unique file access and semantics.
void	h5_write_eigenfield (const std::string &file_name, const Epetra_Comm &comm, mesh::TetMesh tetmesh, NedelecMesh &nedelecmesh, const Epetra_MultiVector &Q, double lambda)
	Write the sampled electric and magnetic fields into the HDF5 file; the function must be called collectively.
void	h5_write_eigenvalue (const std::string &file_name, const Epetra_Comm &comm, mesh::TetMesh tetmesh, NedelecMesh &nedelecmesh, const Epetra_MultiVector &Q, double lambda)
	Write the eigenvalues stored in 'lambda' into the HDF5 file.

Function Documentation

void h5_cartesian_sampling	(	const std::string &	file_name,
		const Epetra_Comm &	comm,
		mesh::TetMesh *	tetmesh,
		NedelecMesh &	nedelecmesh,
		const Epetra_MultiVector &	Q,
		double *	lambda,
		double	xmin,
		double	xmax,
		int	nx,
		double	ymin,
		double	ymax,
		int	ny,
		double	zmin,
		double	zmax,
		int	nz
	)

evaluate the eigenmodal solution on a cartesian grid

provide functionality for mesh and eigenmodal solution access

Retrieve access to paralleltetmesh class instance

Retrieve fine element basis function for the edges and faces, via NedelecMesh.

nedelecmesh is a singleton

Retrieve FE approximation order and number of DoF

Retrieve finite element approximation order, valid throughout the mesh

Retrieve number of DoF associated with the element

Build a new vector to hold required elements

Build an import object for getting the required distributed vector elements from the other processes

Import the distributed vector elements

provide a 3-dimensional arrays of type unsigned int for storing if a specific location is located on the local processor: 0 means no, 1 means yes; this is used because I encountered difficulty with using a boolean type in HDF5.

loop over all cartesian sampling locations and find out if the respective location exists on the local processor; if yes, set the the respective boolean flag true, loop over all modes and compute the electric and magnetic field vectors

we loop over all computed modes

provide two 3-dimensional arrays for storing the electric and magnetic field computed at the respective location

compute sampling interval

prepare the Epetra_Vectors

loop over x-axis

retrieve the tetrahedron that contains the current sampling location

evaluate the eigenmodal field for all modes at the current location

Retrieve DoF vector required for base function evaluation; based on code in nedelecmesh::eval(...)

evaluate the electric field

evaluate the magnetic field

there is no tetrahedron containing the current cartesian sampling position on this processor

end of loop over z-axis

end of loop over y-axis

end of loop over z-axis

store cartesian samples into HDF5 file

Definition at line 1847 of file h5_tools.cpp.

References mesh::TetMesh::construct_octree(), mesh::TetMesh::find_tets_by_point(), NedelecElement::get_dof_ids(), NedelecMesh::get_element(), mesh::Entity::get_id(), NedelecElement::get_order(), h5_cartesian_sampling_write_hdf5(), h5_write_eigenfield_retrieve_DoF_robust(), mesh::ID_NONE, NedelecMesh::map_dof(), x, and y.

Referenced by FemaxxDriver::run().

Here is the call graph for this function:

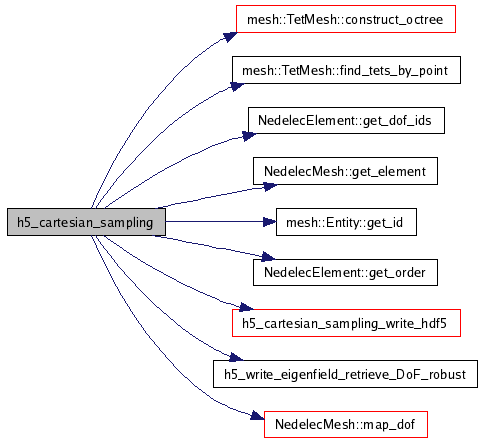
void h5_cartesian_sampling_write_hdf5	(	const Epetra_Comm &	comm,
		const std::string &	file_name,
		unsigned int	nmode,
		std::vector< std::vector< std::vector< unsigned int > > > &	exists,
		std::vector< std::vector< std::vector< std::vector< mesh::Vector3 > > > > &	efield,
		std::vector< std::vector< std::vector< std::vector< mesh::Vector3 > > > > &	hfield,
		double	xmin,
		double	xmax,
		const int	nx,
		double	ymin,
		double	ymax,
		const int	ny,
		double	zmin,
		double	zmax,
		const int	nz
	)

processorwise store the eigenmodal solution, sampled on a cartesian grid, into the hdf5 file; nota bene: because the sequence of access to the hdf5 file is in no way ordered, we must make sure that spatial positions marked as existent by one processor are not overwritten as non-existent by another processor. This is ensured as follows: (1) the root process only initializes the complete 3-dimensional boolean array as false (2) all processors only write into the file if the respective boolean flag signals that the position exists on the local processor; otherwise they do nothing to the hdf5 file.

open the hdf5 file create a new group called eigenmodes_cartesian, within it create the following datasets:

1. dataset : cartesian_limits - a 3 by 2 array contains xmin, xmax ymin, ymax zmin, zmax

2. dataset : cartesian_number_samples - a 3 by 1 array conains nx, ny, nz

3. dataset : cartesian_exists - a 3-dimensional array of type boolean signaling if the a the electric and magnetic field has been sampled at this specific location

4. dataset : cartesian_efield_mode_0 - a 4 dimensional array that stores the electric and magnetic field vector components if it exists and 0 otherwise

dataset : cartesian_hfield_mode_0 - a 4 dimensional array that stores the electric and magnetic field vector components if it exists and 0 otherwise

dataset : cartesian_efield_mode_(k) - a 4 dimensional array that stores the electric and magnetic field vector components if it exists and 0 otherwise

dataset : cartesian_hfield_mode_(k) - a 4 dimensional array that stores the electric and magnetic field vector components if it exists and 0 otherwise

declare MPI related variables

declare variables used for HDF5 access

create the group for storing the cartesian sampled data and write the data defining the cartesian grid sampling. It is essential that this is only done by one single process, ideally the master process.

Set up file access property list with parallel I/O access

create the new group for storing the eigenmodal solution sampled on a cartesian grid

create the datasets for storing cartesian limits

write data

close the dataset

create the datasets for storing the number of samples in respective axis directions

write data

close the dataset

create the datasets for storing the number of modes stored in the eigenmodes_cartesian group

write data

close the dataset

write data

Now, store the electric and magnetic field components into the HDF5 file if the respective location exists on the local processor; we have implemented this using the hyperslab concept, also used in the function h5_write_eigenpoint; this ensures that only those sample vectors are written which need to be written.

compute the number of cartesian locations which need to be written this processor; we just count the number of ones in the 3-dimensional array exists for this.

the local number of cartesian locations to be written into the file

all processors now open the HDF5 file for write access Set up file access property list with parallel I/O access

Set up file access property list with parallel I/O access

create the new group for storing the eigenmodal solution sampled on a cartesian grid

loop over the modes and store the cartesian samples eigenmodal fields into the respective dataset

transform the integer number denoting the mth mode into a string

build the dataset name for the mth mode

create the dataspace for storing a 3-dimensional array of 3-dimensional vectors

collect the data to be written into the file by the specific processor; we use the hyperslab concept, already used in the function h5_write_eigenpoint

Each process defines a dataset in memory and writes it to the hyperslab in the file

the count says how large the hyperslab is in terms of array indices

loop over all cartesian sampling locations

we may only work if the location is on this processor, otherwise no action is allowd

determine offset within the DIM3D+1 dimensional array

transfer the respective data into the array that is written into the file, patterned by the set of hyperslabs

Create property list for collective dataset write

Free dynamically allocated data, if any

close the cartesian eigenmmodal solution group and the file itself

Definition at line 2072 of file h5_tools.cpp.

References DIM2D, DIM3D, H5_GROUP_NAME_EIGENMODES_CARTESIAN(), H5_NAME_FEMAX_EIGENOMDES_CARTESIAN_EFIELD_MODE(), H5_NAME_FEMAX_EIGENOMDES_CARTESIAN_EXISTS(), H5_NAME_FEMAX_EIGENOMDES_CARTESIAN_HFIELD_MODE(), H5_NAME_FEMAX_EIGENOMDES_CARTESIAN_LIMITS(), H5_NAME_FEMAX_EIGENOMDES_CARTESIAN_NMODE(), H5_NAME_FEMAX_EIGENOMDES_CARTESIAN_NUMBER_SAMPLES(), MPIROOTPROCESS, and NREALCOORD3D.

Referenced by h5_cartesian_sampling().

Here is the call graph for this function:

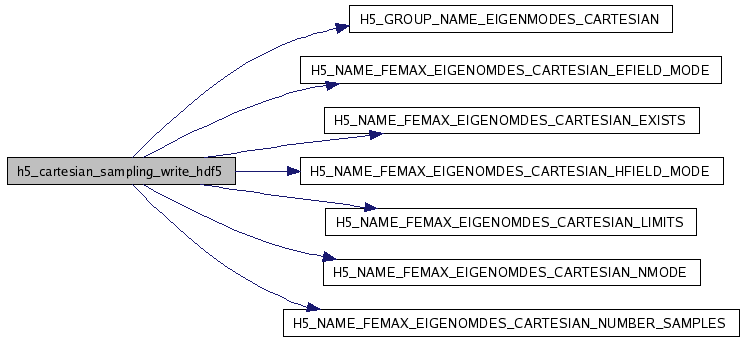
void h5_compute_eigenquality	(	const std::string &	file_name,
		const Epetra_Comm &	comm,
		mesh::TetMesh *	tetmesh,
		NedelecMesh &	nedelecmesh,
		const Epetra_MultiVector &	Q,
		double *	lambda,
		double *&	quality
	)

Compute the quality factor associated with an eigenmode and store it into the HDF5 file.

We note that the eigenvectors have been normalized so that the energy calculated from the respective eigenvector equals unity; the quality factor of the cavity w.r.t a specfic mode is calculated according to the the algorithm given in Ramo, Whinnery, van Duzer, pp. 493, section 10.3, by ecploiting the fact that the magnetic field is zero when the electric field reaches its maximum value; therefore, using the definition of the quality factor $q = {{0} Energy stored}{average power loss} we most only evaluate the magnetic field from which we calculate the surface current density on the cavity's wall; we can the compute the ratio as given above which delivers the cavity's quality factor associated with a specific cavity mode.

We need to keep in mind that all the processors provide contributions to the curls surface integral that must be summed up through a reduce operation in MPI speak.

Furthermore, we use the expressions for the skin depth and surface resistance given in Ramo et al., pp. 151ff. for the calculation of average power loss.

Retrieve access to paralleltetmesh class instance

Retrieve fine element basis function for the edges and faces, via NedelecMesh.

nedelecmesh is a singleton

Open file collectively and release property list identifier

store the rank of this prcocess within this MPI communicator

store the size of an MPI communicator, i.e. the number of processes engaged

Retrieve FE approximation order and number of DoF

Retrieve finite element approximation order, valid throughout the mesh

Retrieve number of DoF associated with the element

Build a new vector to hold required elements

Build an import object for getting the required distributed vector elements from the other processes

Import the distributed vector elements

Definition at line 1574 of file h5_tools.cpp.

References EPSILON_ZERO, NedelecMesh::get_element(), mesh::TetMesh::get_tet(), mesh::Face::get_tet_id(), mesh::Face::get_tet_ids(), h5_write_eigenfield_retrieve_DoF_robust(), mesh::ID_NONE, NedelecMesh::map_dof(), MU_ZERO, mesh::Entity::on_boundary(), mesh::Entity::on_symmetry_planes(), PI, SIGMA_CU_PSI, SPEED_OF_LIGHT_VACUUM, mesh::TetMesh::surface_begin(), and mesh::TetMesh::surface_end().

Referenced by h5_write_eigenvalue().

Here is the call graph for this function:

void h5_create_empty_file ( const std::string & file_name )

End of forward declarations

Definition at line 130 of file h5_tools.cpp.

Referenced by FemaxxDriver::calculate_eigenfields(), and FemaxxDriver::run().

void h5_read_eigenmesh ( const std::string & file_name )

Read the mesh used for the eigenvalue calculations into HDF5 file. The function must be called by alle processes

Definition at line 449 of file h5_tools.cpp.

void h5_read_eigenmodes	(	const std::string &	file_name,
		colarray::Matrix< double > &	Q,
		colarray::ColumnVector< double > &	lambda
	)

Definition at line 404 of file h5_tools.cpp.

References colarray::Matrix< T >::_v, lambda, num_eigenpairs(), and Q.

Here is the call graph for this function:

void h5_read_eigenmodes	(	const std::string &	file_name,
		Epetra_MultiVector **	Q,
		Epetra_SerialDenseVector **	lambda
	)

Definition at line 401 of file h5_tools.cpp.

Referenced by main().

void h5_read_param_list	(	const std::string &	file_name,
		Teuchos::ParameterList &	params
	)

Read parameter list to HDF5 file.

Parameters for the HDF5 are inserted into params.

Definition at line 280 of file h5_tools.cpp.

Referenced by main().

Epetra_Map * h5_write_eigenfeield_retrieve_DoF_efficient	(	const std::string &	file_name,
		const Epetra_Comm &	comm,
		mesh::TetMesh *	tetmesh,
		NedelecMesh &	nedelecmesh,
		const Epetra_MultiVector &	Q,
		double *	lambda
	)

Function used internal to h5_tools by h5_write_eigenfield: retrieve basis functions coefficients, the efficient way

Retrieve access to paralleltetmesh class instance

Retrieve fine element basis function for the edges and faces, via NedelecMesh.

nedelecmesh is a singleton

Retrieve FE approximation order and number of DoF

Retrieve finite element approximation order, valid throughout the mesh

Retrieve number of DoF associated with the element

number of unmapped edge DoF required by this process for base function evaluation

number of unmapped face DoF required by this process for base function evaluation

total number of unmapped DoF

temporary DoF id

Offset required for calculation of id of DoF associated with edges

global edge id

Retrieve number of local DoF, based on FE approximation order

1st order FE approximation

1st order requires as many DoF as there are edges

1st order requires no DoF for faces

The calculation of the local DoF id is based on routines NedelecElement1::get_dof_ids

2nd order requires twice as many DoF as there are edges

2nd order requires thrice as many DoF as there are faces

Initialize DoF id

Retrieve offset required for numbering DoF associated with edge

Every facet has 3 DoF assciated with it

Determine number of actually mapped, i.e. used DoF, and transfer them into a global array

Transfer mapped DoF into arry storing them

build the target map for retrieving the required vector elements.

Definition at line 1007 of file h5_tools.cpp.

References mesh::TetMesh::edge_begin(), mesh::TetMesh::edge_end(), mesh::TetMesh::face_begin(), mesh::TetMesh::face_end(), FIRST_ORDER_FE, NedelecMesh::gdof(), NedelecMesh::get_element(), mesh::TetMesh::get_nof_edges(), mesh::TetMesh::get_nof_faces(), NedelecElement::get_order(), mesh::ID_NONE, NedelecMesh::map_dof(), NCORNERTRIANGLE, and SECOND_ORDER_FE.

Here is the call graph for this function:

void h5_write_eigenfield	(	const std::string &	file_name,
		const Epetra_Comm &	comm,
		mesh::TetMesh *	tetmesh,
		NedelecMesh &	nedelecmesh,
		const Epetra_MultiVector &	Q,
		double *	lambda
	)

Write the sampled electric and magnetic fields into the HDF5 file; the function must be called collectively.

To evaluate the electric and magnetic field at any location within the computational domain, we need the degrees of freedom (DoF) associated with the respective elements; the DoF are the elements of the eigenvectors, resulting from the numerical solution; this eigenvector is an Epetra_MultiVecor, distributed over the processes; therefore, we must make sure that we have on a specific process all the required elements of the eigenvector, especially, we must retrieve the DoF belonging to tetrahedra with facets and edges on interprocessor boundaries; this is accomplished by importing these eigenvector elements with the Epetra import and export commands, cf. the Trilinos tutorial for an introduction. 2006 feb 02, oswald.

store the rank of this prcocess within this MPI communicator

store the size of an MPI communicator, i.e. the number of processes engaged

Retrieve access to paralleltetmesh class instance

Retrieve fine element basis function for the edges and faces, via NedelecMesh.

nedelecmesh is a singleton

Open file collectively and release property list identifier

Retrieve FE approximation order and number of DoF

Retrieve finite element approximation order, valid throughout the mesh

Retrieve number of DoF associated with the element

Build a new vector to hold required elements

Build an import object for getting the required distributed vector elements from the other processes

Import the distributed vector elements

Retrieve local number of tetrahedra

Retrieve location at which electric field shall be sampled

allocate memory to store sampled electric field vectors

allocate memory to store sampled magnetic field vectors

Allocate 1D array for storing the electric field

Allocate 1D array for storing the magnetic field

Used as index for tetrahedra

Retrieve location at which electric field shall be sampled

Retrieve DoF vector required for base function evaluation; based on code in nedelecmesh::eval(...)

retrieve a pointer to the Tet class instance, behave, tit is an iterator, not a pointer

Evaluate the electric field

Evaluate the magnetic field

Store the electric field into an HDF5 file using parallel access mode; the algorithm is similar to the one used in the h5_write_eigenmesh function; we loop over the tetrahedra and store the corresponding electric field vector into the HDF5 file.

Loop over tetrahedra and store electric field into HDF5 file

Free dynamically allocated variables, if any

Definition at line 797 of file h5_tools.cpp.

References NedelecMesh::get_element(), mesh::TetMesh::get_nof_tets(), mesh::ParallelTetMesh::get_num_global_tets(), h5_write_eigenfield_retrieve_DoF_robust(), h5_write_eigenfield_write_hdf5e(), h5_write_eigenfield_write_hdf5h(), h5_write_eigenfield_writehdf5sloc(), mesh::ID_NONE, NedelecMesh::map_dof(), NREALCOORD3D, mesh::TetMesh::tet_begin(), mesh::TetMesh::tet_end(), mesh::Vector3::x, x, mesh::Vector3::y, and mesh::Vector3::z.

Referenced by FemaxxDriver::run().

Here is the call graph for this function:

Epetra_Map * h5_write_eigenfield_retrieve_DoF_robust	(	const Epetra_MultiVector &	Q,
		const Epetra_Comm &	comm
	)

Implementation file for HDF5 tools functionality.

Function used internal to h5_tools by h5_write_eigenfield: retrieve basis functions coefficients, the robust way, i.e to have a simple solution we transfer the global Epetra_MultiVecxtor Q to the local process; while this requires a little bit more memory, it is easier to implement and debug; will be replaced by the more efficien method implemented below.

build the target map for retrieving the required vector elements.

Definition at line 992 of file h5_tools.cpp.

Referenced by h5_cartesian_sampling(), h5_compute_eigenquality(), and h5_write_eigenfield().

void h5_write_eigenfield_write_hdf5e	(	const std::string &	file_name,
		const Epetra_Comm &	comm,
		int	ntet,
		int	gntet,
		int	mthmode,
		double *	ev
	)

Internally used function by h5_write_eigenfield: write sampled field into HDF5 formatted file

number of columns in HDF5 file format; 3 for the cartesian components of the electric field

store the rank of this prcocess within this MPI communicator

store the size of an MPI communicator, i.e. the number of processes engaged

__DEBUG__VERBOSE__

Set up file access property list with parallel I/O access

Open the group named H5_GROUP_FEMAX_EIGENMODES in the file, if it exists; it not, then create it.

Create the dataspace for the dataset, including dataset dimensions and 2 additional integers, which are used to signal (i) the rank of the process which wrote a specific tetrahedron and the total number of processes engaged in the write operation; this information can later be used to signal tetrahedral mesh distribution over the processes by corresponding visualization.

Create the dataset with default properties and close filespace; nota bene, if a new dataset shall be created within a group, then use the group's id when calling H5Dcreate!

Each process defines a dataset in memory and writes it to the hyperslab in the file

Store all columsn

Retrieve information to calculate offset of specific process within mpi communicator group

Array has mpi_size elements, stores number of tets over all processes

Compute offset for specific process mpi_rank

__DEBUG__VERBOSE__

Select the hyperslab within the file

Create property list for collective dataset write

Close and release resources

Definition at line 1126 of file h5_tools.cpp.

References DIM2D, H5_NAME_FEMAX_EIGENFIELD(), and NREALCOORD3D.

Referenced by h5_write_eigenfield().

Here is the call graph for this function:

void h5_write_eigenfield_write_hdf5h	(	const std::string &	file_name,
		const Epetra_Comm &	comm,
		int	ntet,
		int	gntet,
		int	mthmode,
		double *	hv
	)

Internally used function by h5_write_eigenfield: write sampled field into HDF5 formatted file

number of columns in HDF5 file format; 3 for the cartesian components of the electric field

store the rank of this prcocess within this MPI communicator

store the size of an MPI communicator, i.e. the number of processes engaged

__DEBUG__VERBOSE__

Set up file access property list with parallel I/O access

Open the group named H5_GROUP_FEMAX_EIGENMODES in the file, if it exists; it not, then create it.

Create the dataset with default properties and close filespace; nota bene, if a new dataset shall be created within a group, then use the group's id when calling H5Dcreate!

Each process defines a dataset in memory and writes it to the hyperslab in the file

Store all columsn

Retrieve information to calculate offset of specific process within mpi communicator group

Array has mpi_size elements, stores number of tets over all processes

Compute offset for specific process mpi_rank

__DEBUG__VERBOSE__

Select the hyperslab within the file

Create property list for collective dataset write

Close and release resources

Definition at line 1244 of file h5_tools.cpp.

References DIM2D, H5_NAME_FEMAX_EIGENCURL(), and NREALCOORD3D.

Referenced by h5_write_eigenfield().

Here is the call graph for this function:

void h5_write_eigenfield_writehdf5sloc	(	const std::string &	file_name,
		const Epetra_Comm &	comm,
		int	ntet,
		int	gntet,
		double *	slocv
	)

Internally used function by h5_write_eigenfield: write locations where field was sampled into HDF5 formatted file

number of columns in HDF5 file format; 3 for the cartesian components of the electric field

store the rank of this prcocess within this MPI communicator

store the size of an MPI communicator, i.e. the number of processes engaged

__DEBUG__VERBOSE__

Set up file access property list with parallel I/O access

Open the group named H5_GROUP_FEMAX_EIGENMODES in the file, if it exists; it not, then create it.

Create the dataset with default properties and close filespace; nota bene, if a new dataset shall be created within a group, then use the group's id when calling H5Dcreate!

Each process defines a dataset in memory and writes it to the hyperslab in the file

Store all columsn

Retrieve information to calculate offset of specific process within mpi communicator group

Array has mpi_size elements, stores number of tets over all processes

Compute offset for specific process mpi_rank

__DEBUG__VERBOSE__

Select the hyperslab within the file

Create property list for collective dataset write

Close and release resources

Definition at line 1358 of file h5_tools.cpp.

References DIM2D, H5_GROUP_FEMAX_EIGENMODES(), H5_NAME_FEMAX_SLOCBASENAME(), and NREALCOORD3D.

Referenced by h5_write_eigenfield().

Here is the call graph for this function:

void h5_write_eigenmesh	(	const std::string &	file_name,
		const Epetra_Comm &	comm,
		mesh::TetMesh *	tetmesh
	)

Write the mesh used for the eigenvalue calculations into HDF5 file. The function must be called by alle processes

standard loop indices

store result code

global number of tetrahedra, distributed over processes

number of tetrahedra local to this process

store global point id

store tetrahedral vertex indices plus process id and number of processes engaged

Retrieve access to paralleltetmesh class instance

Manage HDF5 file operations

Open file collectively and release property list identifier

store the rank of this prcocess within this MPI communicator

store the size of an MPI communicator, i.e. the number of processes engaged

__DEBUG__VERBOSE__

Set up file access property list with parallel I/O access

Create a group named "/eigenmesh" in the file.

Retrieve local number of tetrahedra

Create the dataset with default properties and close filespace; nota bene, if a new dataset shall be created within a group, then use the group's id when calling H5Dcreate!

Each process defines a dataset in memory and writes it to the hyperslab in the file

Store all columsn

Retrieve information to calculate offset of specific process within mpi communicator group

Array has mpi_size elements, stores number of tets over all processes

Compute offset for specific process mpi_rank

__DEBUG__VERBOSE__

Select the hyperslab within the file

Fill data buffer to be stored into the hyperslab; store tetrahedral vertex id's into a 2 dimensional array

We store the indices of the tetrahedron's vertices and addtionally, the rank of the MPI process writing this specific tetrahedron and also the number of processes engaged in this write up; therefore, the format is as follows:

id0 id1 id2 id3 rank size id0 id1 id2 id3 rank size id0 id1 id2 id3 rank size ... ... ... id0 id1 id2 id3 rank size id0 id1 id2 id3 rank size

Loop over tetrahedra and store them into HDF5 file

Increase index w.r.t tetrahedra

Create property list for collective dataset write

__DEBUG__VERBOSE__

Free dynamically allocated data

Close and release resources

Definition at line 455 of file h5_tools.cpp.

References DIM2D, mesh::TetMesh::get_nof_tets(), mesh::ParallelTetMesh::get_num_global_tets(), H5_GROUP_FEMAX_EIGENMESH(), H5_NAME_FEMAX_TETVID(), NCORNERTET, mesh::ParallelTetMesh::point_gid(), mesh::TetMesh::tet_begin(), and mesh::TetMesh::tet_end().

Referenced by FemaxxDriver::run().

Here is the call graph for this function:

void h5_write_eigenmodes	(	const std::string &	file_name,
		const Epetra_MultiVector &	Q,
		const Epetra_SerialDenseVector &	lambda
	)

Read and write eigenmodes to HDF5 file.

This function must be called collectively.

Definition at line 297 of file h5_tools.cpp.

Referenced by FemaxxDriver::calculate_eigenfields().

void h5_write_eigenpoint	(	const std::string &	file_name,
		const Epetra_Comm &	comm,
		mesh::TetMesh *	tetmesh
	)

Write the tetrahedral point coordinates in parallel mode, ensuring unique file access and semantics.

Write the tetrahedral point coordinates into the HDF File; the function must be called collectively; to obtain a correct data layout, so that the tetrahedra defined previously are consistent with the order of the vertices stored, we use the hyperslab concept provided by HDF5.

The algorithm operates like this::

(i) loop over all poins that are accessible to this local process

(ii) find out if they belong to the respective process and mark them appropriately

(iii) write them into HDF5 file using the hyperslab approach

standard loop indices

store result code

global number of tetrahedra, distributed over processes

number of tetrahedra local to this process

store tetrahedral vertex indices plus process id and number of processes engaged

Retrieve access to paralleltetmesh class instance

Manage HDF5 file operations

Open file collectively and release property list identifier

store the rank of this prcocess within this MPI communicator

store the size of an MPI communicator, i.e. the number of processes engaged

Set up file access property list with parallel I/O access

Open the group named "/eigenmesh" in the file, if it exists; it not, then create it.

retrieve global number of points

Global number of points, i.e. sum of all number of points owned by the processes

Create the dataset with default properties and close filespace; nota bene, if a new dataset shall be created within a group, then use the group's id when calling H5Dcreate!

Each process defines a dataset in memory and writes it to the hyperslab in the file

retrieve global number of points

Number of points owned by this local process

Loop over points accesssible to the local process and find if the local process owns it

Retrieve number of points owned by process and create an array to store the coordinates

Loop over all points accessible to the local process

Create a complex hyperslab

Select the hyperslab within the file

Initialize data buffer

Increase number of points owned by process

increase point counter

__DEBUG__VERBOSE__

Create property list for collective dataset write

Free dynamically allocated data, if any

Close and release resources

Definition at line 638 of file h5_tools.cpp.

References DIM2D, mesh::TetMesh::get_nof_points(), mesh::ParallelTetMesh::get_num_global_points(), H5_GROUP_FEMAX_EIGENMESH(), H5_NAME_FEMAX_POINTS(), NCORNERTET, NREALCOORD3D, mesh::TetMesh::point_begin(), mesh::TetMesh::point_end(), and mesh::ParallelTetMesh::point_gid().

Referenced by FemaxxDriver::run().

Here is the call graph for this function:

void h5_write_eigenvalue	(	const std::string &	file_name,
		const Epetra_Comm &	comm,
		mesh::TetMesh *	tetmesh,
		NedelecMesh &	nedelecmesh,
		const Epetra_MultiVector &	Q,
		double *	lambda
	)

Write the eigenvalues stored in 'lambda' into the HDF5 file.

Typically, the number of eigenvalues is much smaller than the number of elements present in an eigenvector, e.g. 5 or so, therefore, we just use the rank 0 process to write this tiny array into the HDF5 file; its number of rows can later be used to denote the number of eigenmodes present in the output HDF5 file by any postprocessing program. The eigenfrequency is calculate from the eigenvalue through = {} {c_{0}}{2 }.

store the rank of this prcocess within this MPI communicator

store the size of an MPI communicator, i.e. the number of processes engaged

Set up file access property list with parallel I/O access

Create the group named H5_GROUP_FEMAX_EIGENMODES in the file, if it exists; it not, then create it.

Create property list for collective dataset write

Definition at line 1482 of file h5_tools.cpp.

References DIM2D, h5_compute_eigenquality(), H5_GROUP_FEMAX_EIGENMODES(), H5_NAME_FEMAX_EIGENVALUE(), MPIROOTPROCESS, PI, and SPEED_OF_LIGHT_VACUUM.

Referenced by FemaxxDriver::run().

Here is the call graph for this function:

void h5_write_param_list	(	const std::string &	file_name,
		const Teuchos::ParameterList &	params
	)

src/h5_tools.cpp File Reference

Functions

Function Documentation