SquarePolynomialVector describes a vector of multivariate polynomials. More...

#include <SquarePolynomialVector.h>

Collaboration diagram for interpolation::SquarePolynomialVector:

Public Member Functions
	SquarePolynomialVector ()

	SquarePolynomialVector (const SquarePolynomialVector &pv)

SquarePolynomialVector &	operator= (const SquarePolynomialVector &)=default

	SquarePolynomialVector (int pointDimension, MMatrix< double > polynomialCoefficients)

	SquarePolynomialVector (std::vector< PolynomialCoefficient > coefficients)

	~SquarePolynomialVector ()

void	SetCoefficients (int pointDim, MMatrix< double > coeff)

void	SetCoefficients (std::vector< PolynomialCoefficient > coeff)

void	SetCoefficients (MMatrix< double > coeff)

MMatrix< double >	GetCoefficientsAsMatrix () const

void	F (const double point, double value) const

void	F (const MVector< double > &point, MVector< double > &value) const

SquarePolynomialVector	Deriv (const int *derivPower) const

unsigned int	PointDimension () const

unsigned int	ValueDimension () const

unsigned int	PolynomialOrder () const

SquarePolynomialVector *	Clone () const

MVector< double > &	MakePolyVector (const MVector< double > &point, MVector< double > &polyVector) const

double *	MakePolyVector (const double point, double polyVector) const

void	PrintHeader (std::ostream &out, char int_separator='.', char str_separator=' ', int length=14, bool pad_at_start=true) const

Static Public Member Functions
static std::vector< int >	IndexByPower (int index, int nInputVariables)

static std::vector< int >	IndexByVector (int index, int nInputVariables)

static unsigned int	NumberOfPolynomialCoefficients (int pointDimension, int order)

static void	PrintHeaders (bool willPrintHeaders)

template<class Container >
static void	PrintContainer (std::ostream &out, const Container &container, char T_separator, char str_separator, int length, bool pad_at_start)

Static Private Member Functions
static void	IndexByPowerRecursive (std::vector< int > check, size_t check_index, size_t poly_power, std::vector< std::vector< int > > &nearby_points)

Private Attributes
int	_pointDim

MMatrix< double >	_polyCoeffs

Static Private Attributes
static std::vector< std::vector< std::vector< int > > >	_polyKeyByPower

static std::vector< std::vector< std::vector< int > > >	_polyKeyByVector

static bool	_printHeaders =true

Friends
std::ostream &	operator<< (std::ostream &, const SquarePolynomialVector &)

Detailed Description

SquarePolynomialVector describes a vector of multivariate polynomials.

SquarePolynomialVector, an arbitrary order polynomial vector class.

Consider the vector of multivariate polynomials \(y_i = a_0 + Sum (a_j x^j)\) i.e. maps a vector \(\vec{x}\) onto a vector \(\vec{y}\) with
\(\vec{y} = a_0 + sum( a_{j_1j_2...j_n} x_1^{j_1} x_2^{j_2} ... x_n^{j_n})\). Also algorithms to map a single index J into \(j_1...j_n\).

PolynomialVector represents the polynomial coefficients as a matrix of doubles so that
\( \vec{y} = \mathbf{A} \vec{w} \)
where \(\vec{w}\) is a vector with elements given by
\( w_i = x_1^{i_1} x_2^{i_2} ... x_n^{i_n} \)
So the index \( i \) is actually itself a vector. The vectorisation of \( i \) is handled by IndexByPower and IndexByVector methods. IndexByPower gives an index like:
\( w_i = x_1^{i_1} x_2^{i_2} ... x_n^{i_n} \)
While IndexByVector gives an index like:
\( w_i = x_{i_1}x_{i_2} \ldots x_{i_n} \)

Nb: it is a *Square*PolynomialVector because coefficients include all polynomial coefficients with \( i_ j <= n \); coefficients sit within an n-dimensional square. The distinction should be made with a PolynomialVector where coefficients include all polynomial coefficients with \( \Sigma(i_j) <= n. \)

Nb2: It is quite tricky to get right - mostly an excercise in indexing, but that is very easy to get wrong.

Definition at line 71 of file SquarePolynomialVector.h.

Constructor & Destructor Documentation

◆ SquarePolynomialVector() [1/4]

interpolation::SquarePolynomialVector::SquarePolynomialVector ( )

Default constructor

Leaves everything empty, call SetCoefficients to set up properly.

Definition at line 48 of file SquarePolynomialVector.cpp.

Referenced by Clone().

◆ SquarePolynomialVector() [2/4]

interpolation::SquarePolynomialVector::SquarePolynomialVector ( const SquarePolynomialVector & pv )

Copy constructor

Definition at line 52 of file SquarePolynomialVector.cpp.

References _polyCoeffs, and SetCoefficients().

Here is the call graph for this function:

◆ SquarePolynomialVector() [3/4]

interpolation::SquarePolynomialVector::SquarePolynomialVector	(	int	pointDimension,
		MMatrix< double >	polynomialCoefficients
	)

Construct polynomial vector passing polynomial coefficients as a matrix.

Definition at line 59 of file SquarePolynomialVector.cpp.

References SetCoefficients().

Here is the call graph for this function:

◆ SquarePolynomialVector() [4/4]

interpolation::SquarePolynomialVector::SquarePolynomialVector ( std::vector< PolynomialCoefficient > coefficients )

Construct polynomial vector passing polynomial coefficients as a list of PolynomialCoefficient objects.

Any coefficients missing from the vector are set to 0. Maximum order of the polynomial is given by the maximum order of the coefficients in the vector.

Definition at line 64 of file SquarePolynomialVector.cpp.

References SetCoefficients().

Here is the call graph for this function:

◆ ~SquarePolynomialVector()

interpolation::SquarePolynomialVector::~SquarePolynomialVector ( )

inline

Destructor - no memory allocated so doesn't do anything

Definition at line 100 of file SquarePolynomialVector.h.

Member Function Documentation

◆ Clone()

SquarePolynomialVector* interpolation::SquarePolynomialVector::Clone ( ) const

inline

Polymorphic copy constructor.

This is a special copy constructor for inheritance structures

Definition at line 167 of file SquarePolynomialVector.h.

References SquarePolynomialVector().

Here is the call graph for this function:

◆ Deriv()

SquarePolynomialVector interpolation::SquarePolynomialVector::Deriv ( const int * derivPower ) const

Generate polynomial corresponding to the partial derivative of y

Returns: \( \frac{\partial^{j_1+j_2+\ldots} \vec{y}} {\partial x^j_1 \partial x^j_2 \ldots} \) at some set point \( \vec{x} \).

derivPower is an array with indices of the derivative in the "IndexByPower" style, of length PointDimension()

Definition at line 259 of file SquarePolynomialVector.cpp.

References _pointDim, _polyCoeffs, _polyKeyByPower, interpolation::MMatrix< Tmplt >::num_col(), and interpolation::MMatrix< Tmplt >::num_row().

Here is the call graph for this function:

◆ F() [1/2]

void interpolation::SquarePolynomialVector::F	(	const double *	point,
		double *	value
	)		const

Fill value with \( y_i \) at some set of \( x_i \) (point).

point should be array of length PointDimension(). value should be array of length ValueDimension().

Definition at line 109 of file SquarePolynomialVector.cpp.

References PointDimension(), and ValueDimension().

Here is the call graph for this function:

◆ F() [2/2]

void interpolation::SquarePolynomialVector::F	(	const MVector< double > &	point,
		MVector< double > &	value
	)		const

Fill value with \( y_i \) at some set of \( x_i \) (point).

point should be vector of length PointDimension(). value should be vector of length ValueDimension(). Note that there is no bound checking here.

Definition at line 117 of file SquarePolynomialVector.cpp.

References _polyCoeffs, MakePolyVector(), interpolation::MMatrix< Tmplt >::num_col(), and ValueDimension().

Here is the call graph for this function:

◆ GetCoefficientsAsMatrix()

MMatrix<double> interpolation::SquarePolynomialVector::GetCoefficientsAsMatrix ( ) const

inline

Return the coefficients as a matrix of doubles.

Definition at line 124 of file SquarePolynomialVector.h.

References _polyCoeffs.

◆ IndexByPower()

std::vector< int > interpolation::SquarePolynomialVector::IndexByPower	(	int	index,
		int	nInputVariables
	)

static

Transforms from a 1d index of polynomial coefficients to an nd index.

This is slow - you should use it to build a lookup table. For polynomial term \(x_1^i x_2^j ... x_d^n\) index like [i][j] ... [n] e.g. \(x_1^4 x_2^3 = x_1^4 x_2^3 x_3^0 x_4^0\) = {4,3,0,0}.

Definition at line 164 of file SquarePolynomialVector.cpp.

References _polyKeyByPower, and IndexByPowerRecursive().

Referenced by interpolation::PPSolveFactory::getDerivPoints(), IndexByVector(), and PolynomialOrder().

Here is the call graph for this function:

◆ IndexByPowerRecursive()

void interpolation::SquarePolynomialVector::IndexByPowerRecursive	(	std::vector< int >	check,
		size_t	check_index,
		size_t	poly_power,
		std::vector< std::vector< int > > &	nearby_points
	)

staticprivate

Definition at line 151 of file SquarePolynomialVector.cpp.

Referenced by IndexByPower().

◆ IndexByVector()

std::vector< int > interpolation::SquarePolynomialVector::IndexByVector	(	int	index,
		int	nInputVariables
	)

static

Transforms from a 1d index of polynomial coefficients to an nd index.

This is slow - you should use it to build a lookup table. For polynomial term \(x_i x_j...x_n\) index like [i][j] ... [n] e.g. \(x_1^4 x_2^3\) = {1,1,1,1,2,2,2}

Definition at line 188 of file SquarePolynomialVector.cpp.

References _polyKeyByPower, _polyKeyByVector, and IndexByPower().

Referenced by SetCoefficients().

Here is the call graph for this function:

◆ MakePolyVector() [1/2]

double * interpolation::SquarePolynomialVector::MakePolyVector	(	const double *	point,
		double *	polyVector
	)		const

Make a vector like \((c, x, x^2, x^3...)\).

PolyVector should be of size NumberOfPolynomialCoefficients(). Could be static but faster as member function (use lookup table for _polyKey).

Definition at line 139 of file SquarePolynomialVector.cpp.

References _pointDim, _polyCoeffs, _polyKeyByVector, and interpolation::MMatrix< Tmplt >::num_col().

Here is the call graph for this function:

◆ MakePolyVector() [2/2]

MVector< double > & interpolation::SquarePolynomialVector::MakePolyVector	(	const MVector< double > &	point,
		MVector< double > &	polyVector
	)		const

Make a vector like \((c, x, x^2, x^3...)\). polyVector should be of size NumberOfPolynomialCoefficients(). could be static but faster as member function (use lookup table for _polyKey).

Definition at line 127 of file SquarePolynomialVector.cpp.

References _pointDim, _polyCoeffs, _polyKeyByVector, and interpolation::MMatrix< Tmplt >::num_col().

Referenced by F().

Here is the call graph for this function:

◆ NumberOfPolynomialCoefficients()

unsigned int interpolation::SquarePolynomialVector::NumberOfPolynomialCoefficients	(	int	pointDimension,
		int	order
	)

static

Returns the number of coefficients required for an arbitrary dimension, order polynomial e.g. \(a_0 + a_1 x + a_2 y + a_3 z + a_4 x^2 + a_5 xy + a_6 y^2 + a_7 xz + a_8 yz + a_9 z^2\) => NumberOfPolynomialCoefficients(3,2) = 9 (indexing starts from 0).

Definition at line 206 of file SquarePolynomialVector.cpp.

Referenced by interpolation::PPSolveFactory::getDerivPoints(), SetCoefficients(), and interpolation::SolveFactory::SolveFactory().

◆ operator=()

SquarePolynomialVector& interpolation::SquarePolynomialVector::operator= ( const SquarePolynomialVector & )

default

◆ PointDimension()

unsigned int interpolation::SquarePolynomialVector::PointDimension ( ) const

inline

Length of the input point (x) vector.

Definition at line 154 of file SquarePolynomialVector.h.

References _pointDim.

Referenced by F().

◆ PolynomialOrder()

unsigned int interpolation::SquarePolynomialVector::PolynomialOrder ( ) const

Index of highest power - 0 is const, 1 is linear, 2 is quadratic etc...

Definition at line 253 of file SquarePolynomialVector.cpp.

References _pointDim, _polyCoeffs, IndexByPower(), and interpolation::MMatrix< Tmplt >::num_col().

Here is the call graph for this function:

◆ PrintContainer()

template<class Container >

void interpolation::SquarePolynomialVector::PrintContainer	(	std::ostream &	out,
		const Container &	container,
		char	T_separator,
		char	str_separator,
		int	length,
		bool	pad_at_start
	)

static

Print a sequence: with some string that separates elements of index and some character that pads

The total vector length is the total length of the output, set to < 1 to ignore (means no padding) pad_at_start determines whether to pad at start (i.e. right align) or end (i.e. left align)

Definition at line 229 of file SquarePolynomialVector.cpp.

Referenced by PrintHeader().

◆ PrintHeader()

void interpolation::SquarePolynomialVector::PrintHeader	(	std::ostream &	out,
		char	int_separator = `'.'`,
		char	str_separator = `' '`,
		int	length = `14`,
		bool	pad_at_start = `true`
	)		const

Write out the header (PolynomialByPower index for each element).

Definition at line 220 of file SquarePolynomialVector.cpp.

References _pointDim, _polyCoeffs, _polyKeyByPower, interpolation::MMatrix< Tmplt >::num_col(), and PrintContainer().

Here is the call graph for this function:

◆ PrintHeaders()

static void interpolation::SquarePolynomialVector::PrintHeaders ( bool willPrintHeaders )

inlinestatic

Control the formatting of the polynomial vector.

If PrintHeaders is true, then every time I write a PolynomialVector it will write the header also (default).

Definition at line 217 of file SquarePolynomialVector.h.

References _printHeaders.

◆ SetCoefficients() [1/3]

void interpolation::SquarePolynomialVector::SetCoefficients	(	int	pointDim,
		MMatrix< double >	coeff
	)

Reinitialise the polynomial vector with new point (x) dimension and coefficients

Definition at line 69 of file SquarePolynomialVector.cpp.

References _pointDim, _polyCoeffs, _polyKeyByVector, IndexByVector(), and interpolation::MMatrix< Tmplt >::num_col().

Referenced by interpolation::SolveFactory::PolynomialSolve(), and SquarePolynomialVector().

Here is the call graph for this function:

◆ SetCoefficients() [2/3]

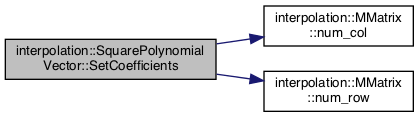
void interpolation::SquarePolynomialVector::SetCoefficients ( MMatrix< double > coeff )

Set the coefficients.

This method can't be used to change point dimension or value dimension - any range mismatch will be ignored.

Definition at line 102 of file SquarePolynomialVector.cpp.

References _polyCoeffs, interpolation::MMatrix< Tmplt >::num_col(), and interpolation::MMatrix< Tmplt >::num_row().

Here is the call graph for this function:

◆ SetCoefficients() [3/3]

void interpolation::SquarePolynomialVector::SetCoefficients ( std::vector< PolynomialCoefficient > coeff )

Reinitialise the polynomial vector with new point (x) dimension and coefficients.

Any coefficients missing from the vector are set to 0. Maximum order of the polynomial is given by the maximum order of the coefficients in the vector.

Definition at line 77 of file SquarePolynomialVector.cpp.

References _pointDim, _polyCoeffs, _polyKeyByVector, IndexByVector(), interpolation::MMatrix< Tmplt >::num_col(), and NumberOfPolynomialCoefficients().

Here is the call graph for this function:

◆ ValueDimension()

unsigned int interpolation::SquarePolynomialVector::ValueDimension ( ) const

inline

Length of the output value (y) vector.

Definition at line 157 of file SquarePolynomialVector.h.

References _polyCoeffs, and interpolation::MMatrix< Tmplt >::num_row().

Referenced by F().

Here is the call graph for this function:

Friends And Related Function Documentation

◆ operator<<

std::ostream& operator<<	(	std::ostream &	,
		const SquarePolynomialVector &
	)

friend

Write out the PolynomialVector (effectively just polyCoeffs).

Definition at line 213 of file SquarePolynomialVector.cpp.

Member Data Documentation

◆ _pointDim

int interpolation::SquarePolynomialVector::_pointDim

private

Definition at line 249 of file SquarePolynomialVector.h.

Referenced by Deriv(), MakePolyVector(), PointDimension(), PolynomialOrder(), PrintHeader(), and SetCoefficients().

◆ _polyCoeffs

MMatrix<double> interpolation::SquarePolynomialVector::_polyCoeffs

private

Definition at line 250 of file SquarePolynomialVector.h.

Referenced by Deriv(), F(), GetCoefficientsAsMatrix(), MakePolyVector(), PolynomialOrder(), PrintHeader(), SetCoefficients(), SquarePolynomialVector(), and ValueDimension().

◆ _polyKeyByPower

std::vector< std::vector< std::vector< int > > > interpolation::SquarePolynomialVector::_polyKeyByPower

staticprivate

Definition at line 251 of file SquarePolynomialVector.h.

Referenced by Deriv(), IndexByPower(), IndexByVector(), and PrintHeader().

◆ _polyKeyByVector

std::vector< std::vector< std::vector< int > > > interpolation::SquarePolynomialVector::_polyKeyByVector

staticprivate

Definition at line 252 of file SquarePolynomialVector.h.

Referenced by IndexByVector(), MakePolyVector(), and SetCoefficients().

◆ _printHeaders

bool interpolation::SquarePolynomialVector::_printHeaders =true

staticprivate

Definition at line 253 of file SquarePolynomialVector.h.

Referenced by PrintHeaders().

The documentation for this class was generated from the following files:

/Users/gsell/src/OPAL/src/src/Classic/Fields/Interpolation/SquarePolynomialVector.h
/Users/gsell/src/OPAL/src/src/Classic/Fields/Interpolation/SquarePolynomialVector.cpp

Public Member Functions

Static Public Member Functions

Static Private Member Functions

Private Attributes

Static Private Attributes

Friends

Detailed Description

Constructor & Destructor Documentation

◆ SquarePolynomialVector() [1/4]

◆ SquarePolynomialVector() [2/4]

◆ SquarePolynomialVector() [3/4]

◆ SquarePolynomialVector() [4/4]

◆ ~SquarePolynomialVector()

Member Function Documentation

◆ Clone()

◆ Deriv()

◆ F() [1/2]

◆ F() [2/2]

◆ GetCoefficientsAsMatrix()

◆ IndexByPower()

◆ IndexByPowerRecursive()

◆ IndexByVector()

◆ MakePolyVector() [1/2]

◆ MakePolyVector() [2/2]

◆ NumberOfPolynomialCoefficients()

◆ operator=()

◆ PointDimension()

◆ PolynomialOrder()

◆ PrintContainer()

◆ PrintHeader()

◆ PrintHeaders()

◆ SetCoefficients() [1/3]

◆ SetCoefficients() [2/3]

◆ SetCoefficients() [3/3]

◆ ValueDimension()

Friends And Related Function Documentation

◆ operator<<

Member Data Documentation

◆ _pointDim

◆ _polyCoeffs

◆ _polyKeyByPower

◆ _polyKeyByVector

◆ _printHeaders