#include <MapAnalyser.h>
Public Types | |
| typedef FMatrix< double, 6, 6 > | fMatrix_t |
| typedef FMatrix< std::complex< double >, 6, 6 > | cfMatrix_t |
Public Member Functions | |
| MapAnalyser () | |
| void | linTAnalyze (const fMatrix_t &) |
| void | linSigAnalyze (fMatrix_t &) |
Private Member Functions | |
| void | eigenDecomp_m (const fMatrix_t &M, cfMatrix_t &eigenVal, cfMatrix_t &eigenVec, cfMatrix_t &invEigenVec) |
| cfMatrix_t | getBlockDiagonal_m (const fMatrix_t &M, cfMatrix_t &eigenVecM, cfMatrix_t &invEigenVecM) |
| void | printPhaseShift_m (fMatrix_t &Sigma, fMatrix_t tM, cfMatrix_t &oldN) |
| void | setNMatrix_m (fMatrix_t &M, cfMatrix_t &N, cfMatrix_t &invN) |
| fMatrix_t | createRotMatrix_m (std::array< double, 3 > phi) |
| fMatrix_t | createSkewMatrix_m () |
| fMatrix_t | realPartOfMatrix_m (cfMatrix_t cM) |
| fMatrix_t | imagPartOfMatrix_m (cfMatrix_t cM) |
| cfMatrix_t | complexTypeMatrix_m (fMatrix_t M) |
| cfMatrix_t | invertMatrix_m (const cfMatrix_t &M) |
| void | rearrangeEigen_m (cfMatrix_t &, cfMatrix_t &) |
| void | normalizeEigen_m (cfMatrix_t &eigenVec, cfMatrix_t &invEigenVec) |
Private Attributes | |
| IpplTimings::TimerRef | mapAnalysis_m |
| IpplTimings::TimerRef | bunchAnalysis_m |
Detailed Description
Definition at line 39 of file MapAnalyser.h.
Member Typedef Documentation
◆ cfMatrix_t
| typedef FMatrix<std::complex<double>, 6, 6> MapAnalyser::cfMatrix_t |
Definition at line 43 of file MapAnalyser.h.
◆ fMatrix_t
| typedef FMatrix<double, 6, 6> MapAnalyser::fMatrix_t |
Definition at line 42 of file MapAnalyser.h.
Constructor & Destructor Documentation
◆ MapAnalyser()
| MapAnalyser::MapAnalyser | ( | ) |
Definition at line 40 of file MapAnalyser.cpp.
Member Function Documentation
◆ complexTypeMatrix_m()
|
private |
Definition at line 251 of file MapAnalyser.cpp.
◆ createRotMatrix_m()
|
private |
Definition at line 207 of file MapAnalyser.cpp.
References cos(), Attrib::Distribution::R, and sin().
Referenced by printPhaseShift_m().

◆ createSkewMatrix_m()
|
private |
Definition at line 220 of file MapAnalyser.cpp.
Referenced by printPhaseShift_m().
◆ eigenDecomp_m()
|
private |
Eigen-decomposition of M
\[ \mathbf{M} = \mathbf{E} \mathbf{\Lambda} \mathbf{E}^{-1} \]
- Parameters
-
M Matrix to analyze eigenVal EigenValues of \(\mathbf{M}\) \(\mathbf{\Lambda}\) eigenVec EigenVectors of \(\mathbf{M}\) \(\mathbf{E}\) invEigenVec inverted EigenVectors of \(\mathbf{M}\) \(\mathbf{E}^{-1}\)
Definition at line 46 of file MapAnalyser.cpp.
Referenced by setNMatrix_m().
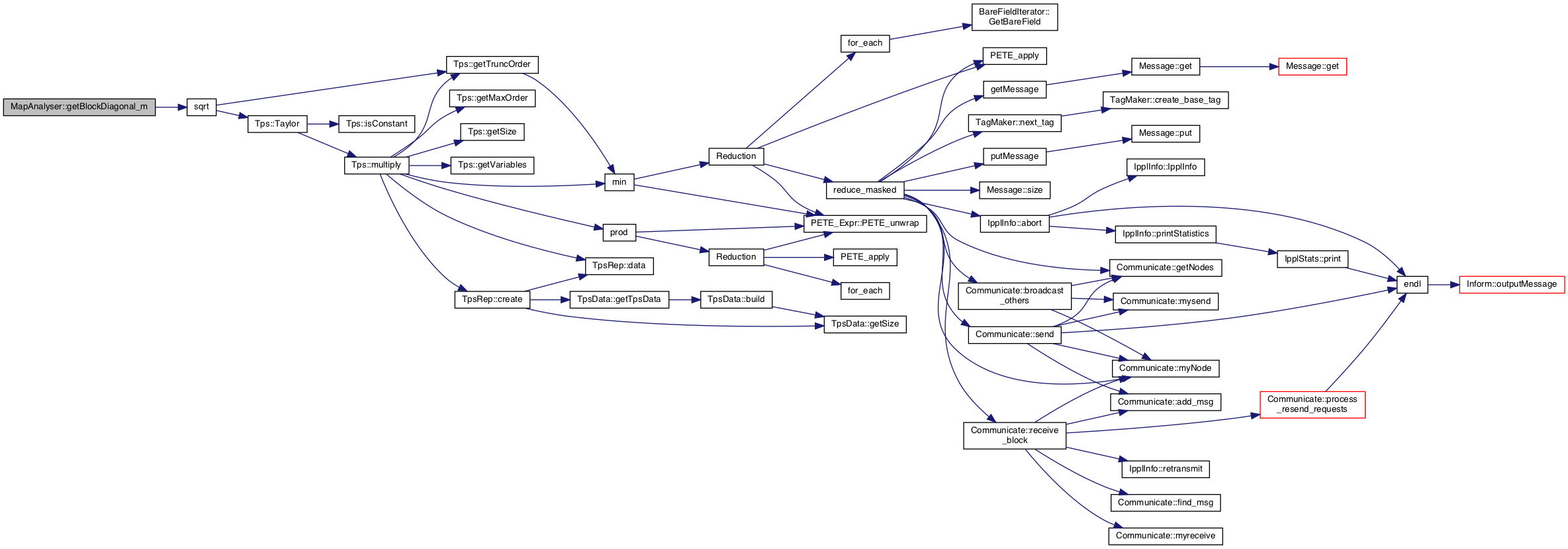
◆ getBlockDiagonal_m()
|
private |
Returns the block diagonal form rotation matrix \( \mathbf{R}\).
This Matrix gets created by applying a symplectic and its inverse Matrix \(U\) on M \( \mathbf{R} = \mathbf{UMU}^{-1}\) [Wolski_2005]
\[ \mathbf{R}_{\left( \mu_x,\mu_y, \mu_z \right)}= \begin{pmatrix} \mathbf{R}_{2\left( \mu_x\right)} & 0 &0 \\ 0 & \mathbf{R}_{2\left( \mu_y\right)} &0 \\ 0 & 0 &\mathbf{R}_{2\left( \mu_z\right)} \end{pmatrix} , \qquad \mathbf{R_2}_{\left( \alpha \right)}= \begin{pmatrix} \cos\left( \alpha \right) & \sin\left( \alpha \right)\\ -\sin\left( \alpha \right) & \cos\left( \alpha \right)\\ \end{pmatrix} \]
- Parameters
-
M Matrix to analyze eigenVec EigenVectors of \(\mathbf{M}\) invEigenVec inverted EigenVectors of \(\mathbf{M}\)
Definition at line 101 of file MapAnalyser.cpp.
References sqrt().
◆ imagPartOfMatrix_m()
|
private |
Definition at line 241 of file MapAnalyser.cpp.
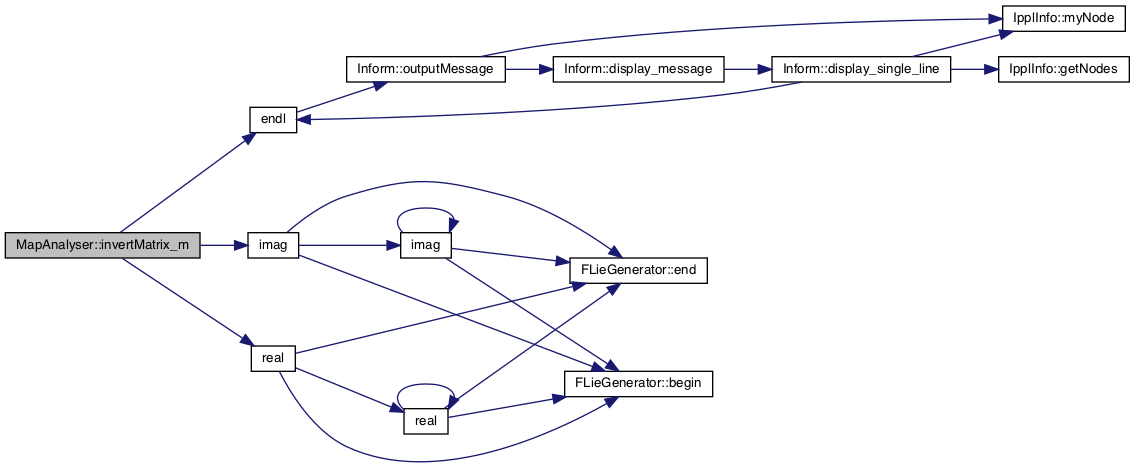
◆ invertMatrix_m()
|
private |
Definition at line 261 of file MapAnalyser.cpp.
References endl(), imag(), and real().
◆ linSigAnalyze()
|
inline |
Analyzes the transfer matrix
@ param sigMatrix Sigma Matrix
Definition at line 60 of file MapAnalyser.h.
◆ linTAnalyze()
|
inline |
Analyzes the transfer matrix for tunes, symplecticity and stability
- Parameters
-
tMatrix Transfer matrix
Definition at line 52 of file MapAnalyser.h.
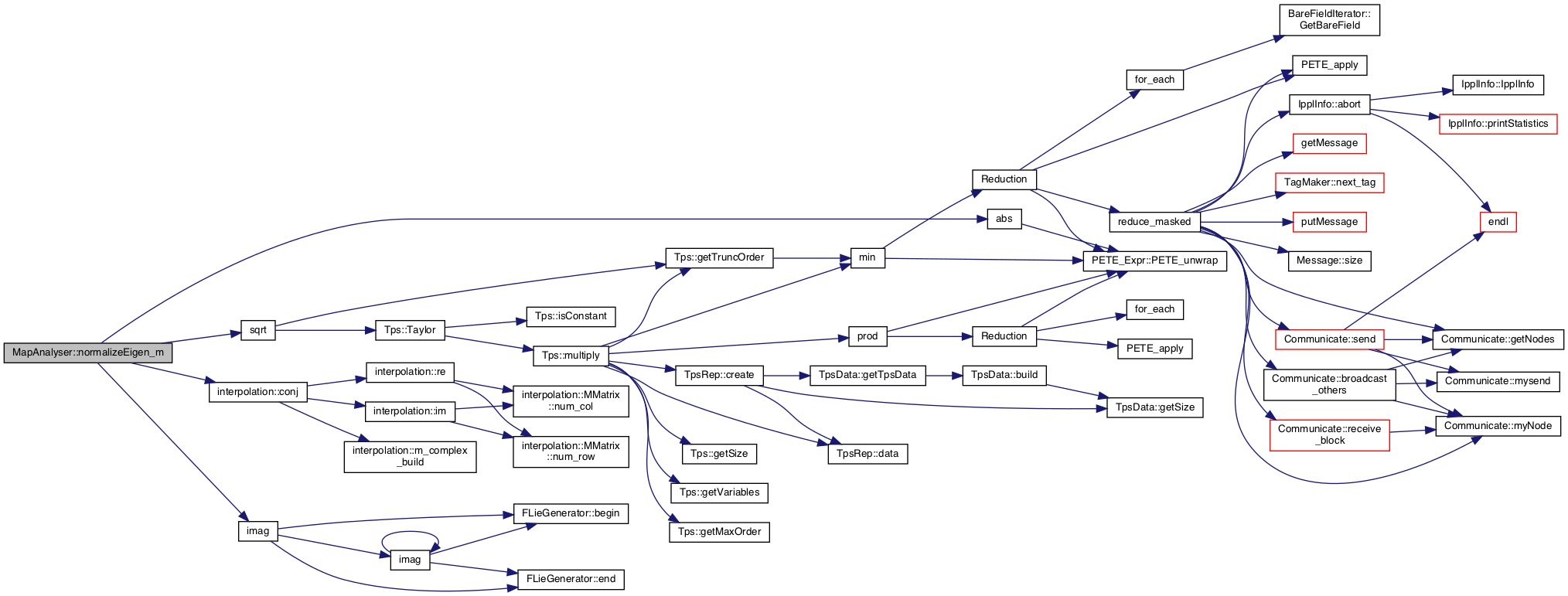
◆ normalizeEigen_m()
|
private |
Definition at line 321 of file MapAnalyser.cpp.
References abs(), interpolation::conj(), Physics::e, imag(), and sqrt().
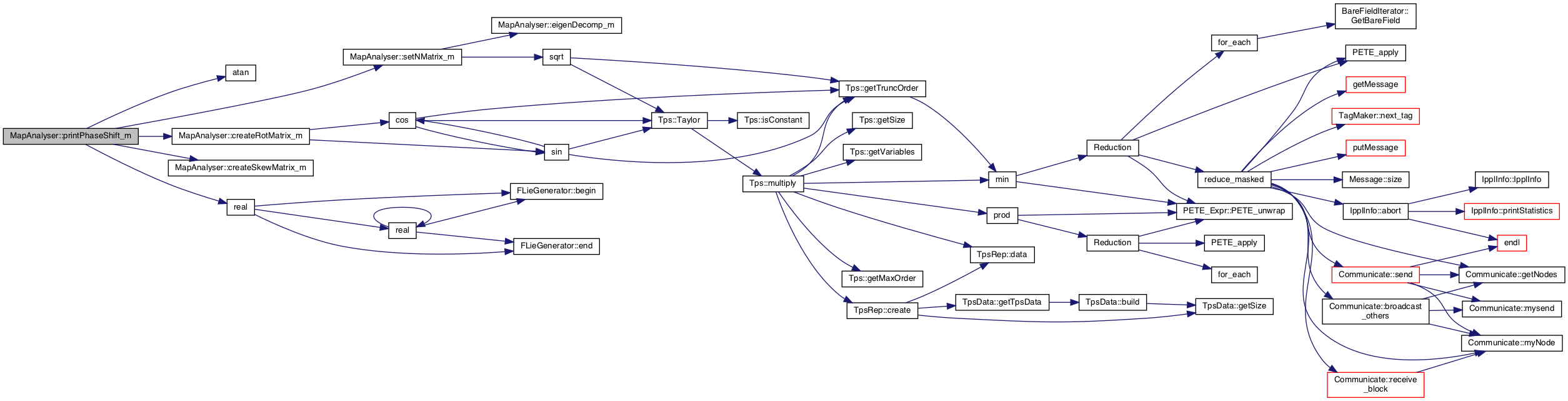
◆ printPhaseShift_m()
|
private |
:TODO: WIP Prints phase shift
- Parameters
-
Sigma Sigma Matirx tM Transfer Matirx oldN \(\mathbf{N}\) matrix
Definition at line 136 of file MapAnalyser.cpp.
References atan(), createRotMatrix_m(), createSkewMatrix_m(), real(), and setNMatrix_m().
◆ realPartOfMatrix_m()
|
private |
Definition at line 231 of file MapAnalyser.cpp.
◆ rearrangeEigen_m()
|
inlineprivate |
Definition at line 135 of file MapAnalyser.h.
◆ setNMatrix_m()
|
private |
sets a symplectic \( \mathbf{N} \) matrix.
This function is a subfunction of ThickTracker::getBlockDiagonal. [Wolski_2005]
- Parameters
-
M Matrix to analyze N symplectic \(\mathbf{N}\) matrix invN inverted symplectic \(\mathbf{N}^{-1}\) matrix
Definition at line 168 of file MapAnalyser.cpp.
References eigenDecomp_m(), and sqrt().
Referenced by printPhaseShift_m().

Member Data Documentation
◆ bunchAnalysis_m
|
private |
Definition at line 141 of file MapAnalyser.h.
◆ mapAnalysis_m
|
private |
Definition at line 140 of file MapAnalyser.h.
The documentation for this class was generated from the following files:
- /Users/gsell/src/OPAL/src/src/Algorithms/MapAnalyser.h
- /Users/gsell/src/OPAL/src/src/Algorithms/MapAnalyser.cpp